The power of exponential growth and M&Ms

The power of exponential growth and M&Ms

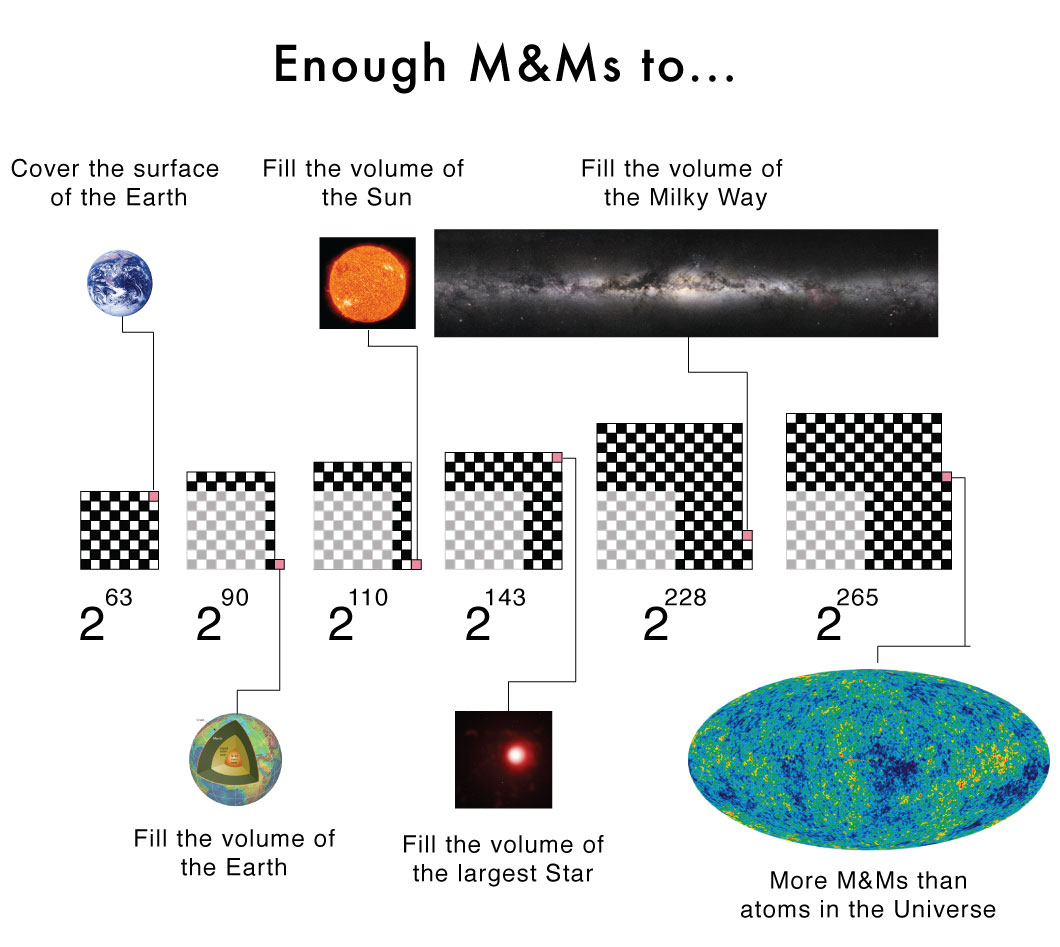
chess-boards-exponential-scaling.jpg

I made an error in my recent TEDxWaterloo talk. Inspired by the legend of Paal Paysam, I used a chessboard and a bowl of M&Ms to illustrate the power of exponential growth. On the first square of the chess board I placed a single M&M, then two on the second square, four on the third square, and so on doubling the number of M&Ms on each subsequent square. Continuing this way I would need 2^63 = 9,223,372,036,854,775,808 M&Ms1 to fill the 64th and final square. If each M&M is approximately 1cm^2 the last square would contain nearly enough M&Ms to cover the surface of the Earth, oceans included, twice over! TEDxWaterloo Krister with Smarties: Photo by Darin White of Makebright.com

But this is not what I said in my talk. I claimed you would need enough M&Ms to fill a bowl the size of the Earth (a volume). There is a big difference between surface area and a volume for a planet-sized object. If we assume2 each M&M is approximately 1 cm^3, then I was off by a factor of about 100 million3. Fortunately, this error does not weaken the argument I was making about the power of exponential growth. A factor of 100 million is large, but how many more times would we need to double the number of M&Ms in order to fill a bowl the size of the Earth? The answer is 27; instead of playing the doubling game on a chessboard with 64 squares we would instead need one with 91 squares. If we are going to add squares, why stop at 91? Here are some interesting numbers that we reach as we continue to add squares to our "super" chessboard.

Exponential scaling demonstrated with doubling periods, a chess board, and M&Ms

  • 111 squares (2^110): Enough M&Ms to fill a bowl the size of the Sun. They will melt pretty quickly.

  • 144 squares (2^143): This is enough M&M to fill a bowl the size of VY Canis Majoris, the largest known star with a radius 2200 times larger than the Sun.

  • 229 squares (2^228): Enough M&Ms to fill a bowl the size of the Milky Way, the galaxy not the chocolate bar, with M&Ms.

  • 266 squares (2^265): More M&Ms than there are atoms in the observable universe!. Various estimates put the number of atoms at ~10^80.

Exponential growth is powerful stuff!

  1. 64 doubling periods corresponds to 2^(64-1)=2^63 M&Ms. The first square contains 2^0=1 M&M. The second square has 2^1=4 M&Ms and so on. For N squares there will be 2^(N-1) M&Ms. ↩
  2. The volume of an M&M is roughly 0.636 cm^3 (see here or here). However, when packing M&M's into a bowl their will be some gaps between them. M&Ms can occupy a maximum of 68% of the volume in a bowl, leaving 32% empty. Therefore an M&M will occupy roughly 1 cm^3 (.636/.68). As a side note, you can fit more M&Ms into a bowl than perfect spheres. This was only discovered a few years ago, but has had a dramatic impact on many different fields. ↩
  3. I originally calculated the right answer (surface area), but before the talk only glanced over my old notes. I somehow got it stuck in my head that I was dealing with the Earth's volume instead of surface area. of course if we lived in the dark ages when the when the Earth was assumed to be flat, then my answer would be correct. ↩

The Quantum Dance

My TEDxWaterloo talk is out! With the help of a magician, a live band, and nearly 500 dancers from around the world, I explain how quantum entanglement can be used to build super fast computers. For more information on how the talk was put together check out the Project Q website.

Each part of the dance represents a different aspect of quantum computing. In the coming days I plan on writing a longer blog post that breaks down the routine and explains what is happening. Stay tuned.

Mr. Rogers Remixed

You can grow things in the garden of your mind.


See also this clip of Mr. Rogers, in 1969, defending PBS in front of congress.

QuTiP: Quantum Toolbox in Python

QuTiP: Quantum Toolbox in Python

jc_model_wigner_49.png

I was recently introduced to the quantum optics toolbox in Matlab, written by Sze Meng Tan, which is useful for quickly programming and studying a variety of quantum optics systems. Despite being great, the toolbox has not been updated since 2002.

Now there is QuTiP, a quantum toolbox for Python that is inspired by Sze's work. This software is actively maintained, and comes with a number of useful features. It is easy to parallelize certain tasks, it is more memory efficient, and it is faster. This toolbox has motivated me to learn Python–a surprisingly easy task. The excellent NumPy and Scipy libraries, along with Matplotlib, replicate most of the functionality found in Matlab with a similar syntax. A convenient way to install Python and the libraries that QuTip needs is to grab a copy of the Enthough Python Distribution, or if you already have Python installed to grab the Scipy Superpack. Note: QuTiP is only supported on Unix based systems like Linux or Mac OS X.

What makes this toolbox so great is that it allows you to write programs in a way that mimics how we write out physics problems. The program has lots of built in quantum opjects, such as annihilation, creation, squeezing, and displacement operators, that allow one to write down a Hamiltonian directly. Wigner and Q functions are built in, making it easy to plot quasi-probability distributions.

For example, this is the code used to create a coherent state.

N= 20 #Size of Hilbert Space 
alpha= 3 #amplitude of the coherent state 
D = displace(N,alpha) # Displacement operator 
vac= basis(N,0).unit() # Vacuum state 
psi=(D*vac).unit() # create a coherent state. The unit() ensures normalization.

It is easy to great operators as well. For example, let's look at how to create the nonstandard squeezing operator \(S3=\frac{1}{2}(\zeta^{\ast} a^{\dagger 3} - \zeta a^3),\) where \(\zeta\) is a squeezing parameter and \(a \) is the annihilation operator.

a = destroy(N) #annihilation operator 
S3=(1/2.0)*conj(zeta)*(a**3)-(1/2.0)*zeta*(a.dag())**3

Note: in Python ** means raise to the exponent. Here a**3 means \(a^3\).

QuTiP stores our operator as an object. One of the built-in methods allows us to exponentiate this operator so we can act on a state. For example, to create a squeezed state we act on the vacuum state with our squeezing operator, S3, and our displacement operator, D.

psi=(D*S3.expm()*vac).unit()

There is an impressive array of examples available from the QuTip website. The authors also have this paper that outlines how the program works, the performance benefits, and some excellent examples.

Here is a simple program I wrote, based on this example in the documentation, to plot the Wigner functions for a series of Schrödinger's cat states (a superposition of two different coherent states). The results are shown in the animated gif below.

# 3D Wigner functions for a series of cat states. #   
from qutip.states import *   
from qutip.Qobj import *   
from qutip.operators import *   
from qutip.wigner import *   
from mpl_toolkits.mplot3d import Axes3D   
from matplotlib import cm   
from pylab import *  

#setup constants: 
N = 20 # size of the Hilbert space 
alpha=linspace(0.01,3,60) # values for the coherent state amplitude 
a = destroy(N) #annihilation operator 
D = displace(N,alpha) # Displacement 
xvec = linspace(-9,9,300) 
X,Y = meshgrid(xvec, xvec)

k=1 # counter 
for x in alpha: 

    # Define the cat state. It is a coherent superposition of two coherent states. 
    # Each coherent state is created by the displacement operator acting on the vacuum. 
    # the unit() function makes sure that the overall state is normalized. 

    psi=(displace(N,x)*basis(N,0)-displace(N,-1*x)*basis(N,0)).unit();

    # plot the wigner function 
    W=wigner(psi,xvec,xvec) 
    fig =figure() 
    ax = Axes3D(fig,azim=-62.5,elev=25) 
    ax.plot_surface(X, Y, W, rstride=2, cstride=2, cmap=cm.jet,lw=.1) 
    ax.set_xlim3d(-9,9) 
    ax.set_xlim3d(-9,9) 
    ax.set_zlim3d(-.2,0.2) 
    ax.set_axis_off() 
    ax.set_frame_on('false') 
    title(r'$| \psi >= \frac{1}{\sqrt{2}}(|\alpha>-|-\alpha>)$'+r' $\alpha=$'+str(round(x,2))) 
    savefig("cat_state_"+str(k)+".png") k=k+1;
Wigner Functions of Schrödinger Cat State Animation

UPDATE: While I was writing this post, version 2 of QuTiP was released. I haven't had a chance to look at the new version in depth, but this looks like a solid update.

Domino Chain Reaction

Today I heard about a neat video Stephen Morris, a prof at the University of Toronto, put together. The idea is that a domino can knock over another domino that is 50% taller than itself. You can use this to build a kind of domino chain reaction where each domino knocks over a larger, subsequent, domino. The initial domino is only 5 mm tall, but after 13 dominos knocks over a massive domino nearly 1 m tall.

That hallway in the physics building at UofT brings back memories.

Peak Babies

Hans Rosling on whether the type of religion (Christianity, Islam, or Eastern religions) is correlated with the average number of children a woman gives birth to.


A great sound bite from the talk:

The number of children [per family] is not growing any longer in the world. We are still debating peak oil, but we have definitely reached peak child.” (Hans Rosling)

Why great ideas come when you aren’t trying

Good to see some research being carried out into this.

As well as revealing that breaks on their own do not encourage creative thinking, Baird’s work suggests an explanation for one of psychology’s great mysteries: why we zone out.

From an evolutionary perspective, mind-wandering seems totally counterproductive and has been viewed as dysfunctional because it compromises people’s performance in physical activities. However, Baird’s work shows that allowing the brain to enter this state when it is considering complex problems can have real benefits. Zoning out may have aided humans when survival depended on creative solutions.

Reminds me of this Google Tech Talk by Nobel laureate Murray Gell-Man "On Getting Creative Ideas"


Spectacular time-lapse of the annular solar eclipse

Spectacular time-lapse of the annular solar eclipse

Sun41600x1200.jpeg

Cory Poole's timelapse of yesterday's annular solar eclipse using a Coronado Solar Max 60 Double Stack telescope and a GH2. The telescope has a built in notch filter that only allows light from the H-alpha line at 656.28 nm to pass through. This allows astronomers to see features from the surface of the sun. 

Cory will be posting photos from the eclipse to his website shortly. He has a beautiful collection of photos available. Check them out.

(Via Kottke.org)

Could You Build a Scale Lego Model of the Death Star?

According to Rhett Allain all you need is two trillion kilograms of lego. That weighs as much as 400 million elephants. Can you imagine trying to launch 400 million elephants into space? In low Earth orbit (~300 km), the scale model Death Star would appear bigger than the moon from earth:

People would mistake it for a moon, just like Han Solo did. Well, it look just like the moon except that it would just take a couple of minutes to pass across the sky where the moon doesn’t really seem to change its position.

Check out the figure that Rhett put together comparing the scale model to the World's tallest buildings.

Why I Am Leaving Goldman Sachs

Wow. Greg Smith submits his resignation letter to Goldman Sachs via the NY Times:

It makes me ill how callously people talk about ripping their clients off. Over the last 12 months I have seen five different managing directors refer to their own clients as “muppets,” sometimes over internal e-mail. Even after the S.E.C., Fabulous Fab, Abacus, God’s work, Carl Levin, Vampire Squids? No humility? I mean, come on. Integrity? It is eroding. I don’t know of any illegal behavior, but will people push the envelope and pitch lucrative and complicated products to clients even if they are not the simplest investments or the ones most directly aligned with the client’s goals? Absolutely. Every day, in fact.

The dark core of dark matter

The dark core of dark matter

nasa-abel-dark-matter.jpg

The link above is an interview I did for CTV's National Affairs on a new result that could change our understanding of dark matter.

Previous evidence points to dark matter not being able to interact with other dark (or regular) matter except weakly through gravity. Researchers at UBC took a look at a "cosmic train wreck" that occurred when two galatic superclusters smashed into one another. These galatic superclusters, each containing hundreds or even thousands of individual galaxies, are mostly made up of free Hydrogen gas. During the collision the gas interacts and gets "stuck" in the middle while the stars, planets, and dark matter should keep on moving through.

In this case it appears that the dark matter gets "stuck" in the middle as well, something that was not seen in previous observations of other cosmic train wrecks. There are a number of possible explanations, all of which will teach us something new about nature of dark matter:

  • Some dark matter may actually be able to interact with other dark matter via some new force.
  • There may have already been a large chunk of dark matter, without much regular matter, sitting in the middle where the collision took place. In this case, we need to understand how so much dark matter can exists without much regular matter.
  • Dark matter has a filament-like nature, similar to how roots on a tree grow. In this case, we may be looking at one of the filaments end on. Imagine looking at a pencil end on. All you would see is the pencil point and not have any idea how long the pencil actually is. A similar thing could be happening with the dark matter–what we see as a small dense core in the center could actually be a an incredibly long filament of dark matter.

This result provides another puzzle piece in the mystery of what dark matter is, how galaxies form, and what our place in the universe is.

A big thanks to Adrienne Erickcek and Keith Vanderlinde for walking me through this exciting work.

Project Q passes 300 participants

With a flurry of videos being submitted last night and today there are now 316 people who have taken part in Project Q! This is far beyond what I had hoped for. Thank you Lindy Hoppers for being so awesome.

Sheldon may play dice, but scientific publishing cannot be left to chance

Sheldon may play dice, but scientific publishing cannot be left to chance

Sheldondice.jpeg

This is a guest post written by a fellow physicist, Marco Piani, who loves quantum information and the TV show The Big Bang Theory In a recent episode of the The Big Bang Theory, "The Wiggly Finger Catalyst", Sheldon reverts to taking "minor" decisions by rolling dice. It does not always work perfectly, as Sheldon, for example, ends up eating food he doesn't really want just because the dice have "decided" so.

 

Nonetheless, Sheldon argues that his mind, not burdened anymore by the consideration of minor issues, can focus better on questions much worthier of Sheldon's attention. He judges his experiment a success, in particular because he is able to publish two papers in "notable peer-reviewed journals" in a short period. The measure of success adopted by Sheldon is actually shared to a good extent by the entire academic system: indeed, one of the main goals of a researcher is that of publishing papers in "good" journals. What does this mean?

A researcher devotes his/her work, for example, to better understand how the world works, to improve the treatment for some disease, or to create some new technology. These results only come with dedication and hard work. When there is enough progress---for example, when a group of astrophysicists have collected enough data about the explosion of a giant star, achieving a better understanding of the life cycle of stars---this progress is reported to the scientific community by means of an article published in a scientific journal---a highly specialized research magazine. Such an article may condense down to few pages years of work.

Roughly speaking, papers constitute the record of the progresses made in science (in all the senses mentioned above, and in many more!) and add to the body of human knowledge. Most importantly, they are used as references---that is, roughly speaking, as the starting point---for the future work of other scientists, as well as for developing applications of scientific knowledge.

It is then quite obvious that published results must be sound: that is, mathematically correct in the case of theory, and supported by the collected data---as well as by the methodology of the data analysis---in the case of experiments. A key issue is that science is divided in so many fields and subfields that only people working on the same or a similar topic can really check that the progresses being reported are, first of all, actually interesting progresses---worth being "archived" and developed in the future---and, most importantly, correct. Hence the notion of "peer-reviewed journals": in order to publish, a researcher has to convince his/her own colleagues that what he/she has done is worth the attention of the scientific community and is correct. Furthermore, the level of "interest" of the results is nowadays often reflected by the journal in which the results are published: "good" journals have a higher bar for what is deemed "interesting".

There are a lot of details and many subtle points that we are leaving out here. For example, the people who have to review a manuscript submitted for publications and to help decide about its acceptance---the "referees"---are often unknown, both to the authors of the manuscripts and to the rest of the community. The idea is that referees can then be less afraid to point out potential issues affecting the submitted paper, while they could restrain themselves from doing it if the persons whose work they are judging today could knowingly end up judging their work in the future.

The principle that whatever new result should be scrutinized by the community of peers is well established; in many ways it is a cornerstone of modern science. On the other hand, the exact process to arrive at the acceptance of new results and to their incorporation into the body of scientific knowledge---as well as the issue of how these results should be made available and disseminated---may change in the near future.

At the moment this process is mainly administered by scientific journals and their editors. It is the editors who receive the request from the authors to publish their manuscript. It is the editors who get in touch with potential referees, asking them to judge the submitted manuscript. It is the editors who, after reading the reviews of the referees, finally choose whether to accept the manuscript for publication. Most importantly, it is often the case that papers appearing in journals---that is, the only papers nowadays "officially" certified as "interesting and correct"---can only be accessed through the payment of a fee.

But exactly in these days many scientists and thinkers (notably Timothy Gowers, a Field medalist 1, and Michael Nielsen, the author of Reinventing discovery, an interesting book about how the Internet will dramatically change the way we do science) are considering how the traditional peer-review process and the scientific publishing industry could be disrupted by new online tools and by the more direct involvement of the community of scientists through these tools.

Sheldon may be happy about letting dice decide about other issues to focus entirely on finding new results, but researchers all around the world are aware that modern science is a very complex and collective enterprise. In particular, new results require both validation and dissemination; while "peer-review journals" have played and still play a primary role in these two processes, things could soon change.

  1. The Field medal is considered the correspondent of the Nobel prize for Mathematics ↩

Latest round of Project Q Submissions

We are up to 206 Lindy Hoppers who have taken part in Project Q! There have been a number of new cities who have submitted videos, and I know of a number of others who are either filming or working on their videos as the deadline approaches. I spent the past weekend working with the dancers, band, and other guests who will take part in the talk. It is going to be amazing. I cannot wait to show everyone the final product.